
Manipulating quantum states on a superconducting chip cooled to a fraction of a degree above absolute zero at the bottom of a cryogenic fridge is incredibly challenging. And things don't always go to plan. Errors happen. Lots of errors. Sophisticated strategies are required to extract reliable computation from what would otherwise be just so many random output bits. Success is only possible if errors are not too overwhelmingly common.
Today, Google Quantum AI announced the construction of a quantum chip where errors are indeed not overwhelmingly common. It makes use of the surface code, essentially a square patch of nearest-neighbor coupled physical qubits that work together to form a single more reliable logical qubit. As the square patch gets bigger, a logical qubit should get more reliable, and that is exactly what we demonstrated: a chip with logical qubits getting over a factor of two more reliable with each increase in patch size.
But why is this needed—what are quantum errors and how are they corrected?
We'll give a short version of the answers here, and if you want more than a brief overview, you can head straight to the hands-on quantum error correction course now available for free on Coursera where you will find a series of videos and exercises to develop your understanding. “This new course opens a door to a complex domain, making quantum error correction not just accessible, but tangible for millions of learners worldwide,” says Marni Baker Stein, Chief Content Officer at Coursera. “Our collaboration with an industry pioneer like Google Quantum AI signifies another step towards a future where knowledge is the key to harnessing the power of quantum computing.”

Let's start with classical errors. You have a bit. Suppose it should be 0. But a cosmic ray hits it and it becomes 1. That's a bit-flip error, the only type of error in a classical computer. In comparison, a quantum chip doesn't consist of bits but rather multilevel quantum systems so cold they have well-defined discrete ground and excited states. We write these states as |0>, |1>, |2>, etc. When a cosmic ray hits a qubit that should be |0>, it can produce a superposition a|0> + b|1> + c|2> + ... of many states. Careful engineering of our device has made our qubits robust to all but the most energetic impacts, allowing us to compute results and simply discard the output when we are hit.
When computing, we try hard to only use states |0> and |1>, but control and measurement errors inevitably lead to the occasional |2+> state, known as leakage errors. Resetting a qubit gets rid of this error, but also gets rid of any data on that qubit, so we have a special gate that moves higher states off data qubits and onto a qubit about to be reset. This prevents the accumulation of |2+> states in the computer.
Then there is the problem that quantum data just doesn't like hanging around very long. Qubits like to relax. If you use an excited state to represent |1>, after a short time it will relax to |0>. We also want to be able to store superpositions like a|0> + b|1>, and that ‘plus’ can spontaneously become a ‘minus’, or a phase-flip error. The various ways that qubits lose data are collectively called decoherence. In general, decoherence can produce a completely different state to the one we want, but fortunately this difference can be broken into a mix of bit flips and phase flips; for brevity we call them X and Z errors.
Let's start with a picture of our quantum chip.
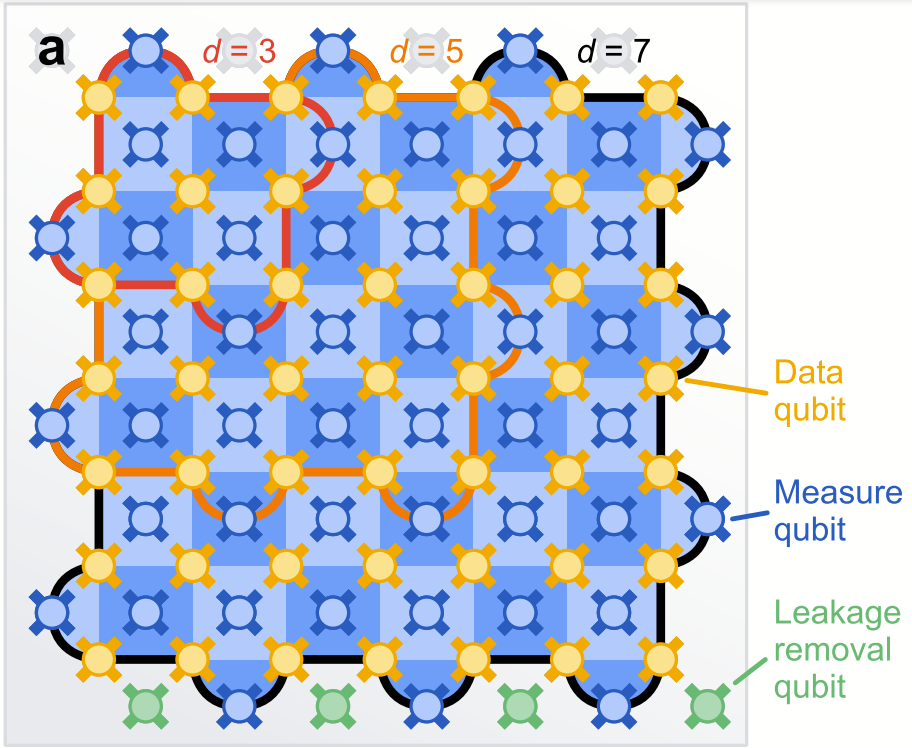
This is a 2D array of qubits with nearest neighbor interactions only. Data qubits store our precious quantum state. Measure qubits are used to detect X and Z errors. A good way to understand this is to imagine each light blue region detecting Z errors on the data qubits it touches, and each dark blue region detecting X errors. A Z error on a data qubit activates the neighboring light blue regions, locating it and allowing us to compensate for its presence in software. Provided the density of X and Z errors is low enough, the pattern of lit up regions will give us clear information allowing us to find and compensate for these errors.
If a measure qubit suffers an error, that can give you a falsely activated region. To cope with this, the search for errors is repeated as often as possible, and the next time the check is performed there is a good chance it will be resolved. This creates an identifiable signature for a measurement error, enabling these to also be handled in software. It is an area of ongoing research to devise more sophisticated algorithms to handle the output of measure qubits to better identify the location and type of errors, all while keeping pace with the quantum computer.
What we’ve covered above is scraping the surface of quantum error correction and the critical role it plays in advancing quantum computing. For a step-by-step explanation and labs starting from the very basics, through quantum states and circuits, to some of the latest error correction tools used today, go to Coursera for our hands-on quantum error correction course.
If you are a software engineer who has always wanted to work on a quantum problem, after taking the course head over to Quantum AI open source tools, where we build open-source software like Cirq, Stim and Crumble to simulate quantum circuits and develop error correction techniques. Learn how to design quantum algorithms and contribute to the development of tools that will enable the realization of practical quantum computing.
Here is an exciting area of research that combines theoretical computer science, software engineering, and quantum physics:
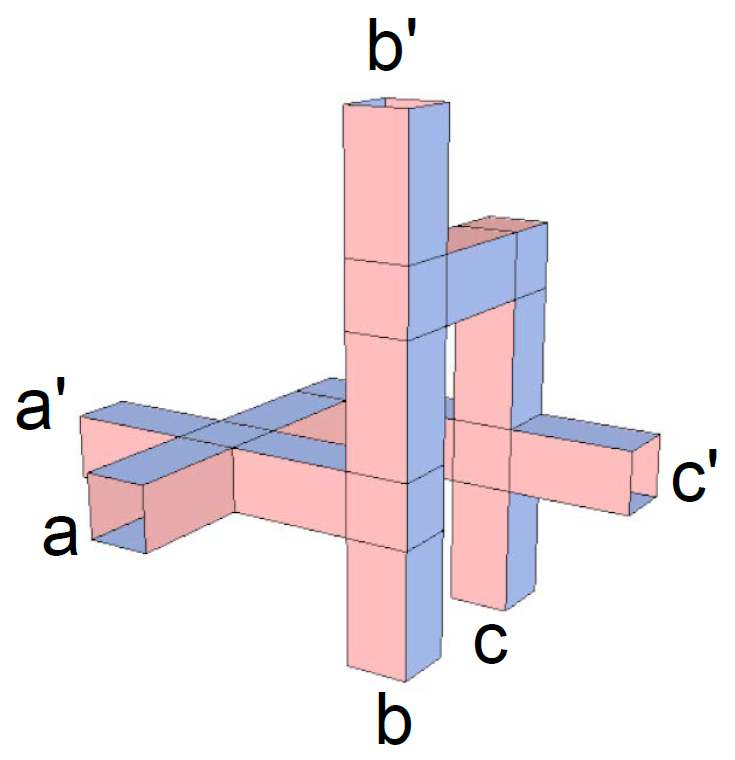
Join this group to get access to the TQEC project and learn why this image is a picture of scalable fault-tolerant quantum computation, three logical qubits abc undergoing three controlled-NOT gates to produce outputs a'b'c'.