Embora o JAX seja bem conhecido como um framework muito utilizado no desenvolvimento de modelos de IA em larga escala, ele também está sendo adotado rapidamente em um conjunto mais amplo de domínios científicos. Estamos particularmente empolgados com seu uso crescente em áreas que exigem muito da computação, como o aprendizado de máquina baseado na física. O JAX dá suporte a transformações de composição, um conjunto de funções de ordem superior. Por exemplo, o grad usa uma função como entrada e retorna outra função que calcula seu gradiente e, o que é mais importante, você pode aninhar (compor) essas transformações livremente. Esse design é o que torna o JAX especialmente elegante para derivadas de ordem superior e outras transformações complexas.
Recentemente, tive o prazer de conversar com Zekun Shi e Min Lin, pesquisadores da Universidade Nacional de Singapura e da Sea AI Lab. A experiência deles ilustra claramente como o JAX pode lidar com desafios fundamentais na pesquisa científica, particularmente em relação ao abismo computacional enfrentado na resolução de equações diferenciais parciais (EDPs) complexas. Sua jornada, desde a batalha com as limitações dos frameworks tradicionais até o uso da diferenciação automática do modo Taylor, exclusiva do JAX, é uma história que interessará muitos pesquisadores.
Nosso trabalho se concentra em uma área desafiadora da computação científica: o uso de redes neurais para resolver EDPs de ordem superior. As redes neurais são aproximadoras de funções universais, o que as torna uma alternativa promissora aos métodos tradicionais, como os elementos finitos. No entanto, um grande obstáculo na resolução de EDPs com uma rede neural é que você precisa avaliar suas derivadas de ordem superior, às vezes até a quarta ordem ou mais, incluindo as derivadas parciais mistas.
Os frameworks padrão de aprendizado profundo, que são otimizados principalmente para modelos de treinamento por meio de retropropagação, não são adequados para essa tarefa, já que a computação de derivadas de ordem superior é incrivelmente cara. O custo da aplicação da retropropagação (diferenciação automática reversa) repetidamente para derivadas de ordem superior aumenta exponencialmente com a ordem de derivadas (k) e polinomialmente com a dimensão de domínio (d). Essa "maldição da dimensionalidade" e o aumento exponencial da ordem de derivadas tornam praticamente impossível trabalhar com problemas grandes e complexos do mundo real.
Embora haja outras bibliotecas populares para o aprendizado profundo, nossa pesquisa exigia um recurso mais fundamental: a diferenciação automática (DA) do modo Taylor. O JAX foi um divisor de águas para nós.
A principal distinção arquitetônica do JAX é o seu poderoso mecanismo de representação e transformação de funções, implementado pelo rastreamento de código Python e compilado para alto desempenho. Esse sistema é projetado com tal generalidade que permite uma gama versátil de aplicações, desde a compilação just-in-time até a computação de derivadas padrão. É essa flexibilidade subjacente que permite operações avançadas que não são facilmente alcançáveis em outros frameworks. Para nós, a aplicação crucial foi o suporte à DA do modo Taylor, um resultado direto e poderoso dessa arquitetura única que torna o JAX perfeitamente equipado para nosso trabalho científico. A DA do modo Taylor permite a computação eficiente de derivadas de ordem superior expandindo ainda mais a série de Taylor de uma função e fazendo a computação eficiente de derivadas de ordem superior em uma única passagem, em vez de por meio da dispendiosa retropropagação repetida. Isso nos permitiu desenvolver um algoritmo, o Stochastic Taylor Derivative Estimator (STDE), para randomizar e estimar de forma eficiente qualquer operador diferencial.
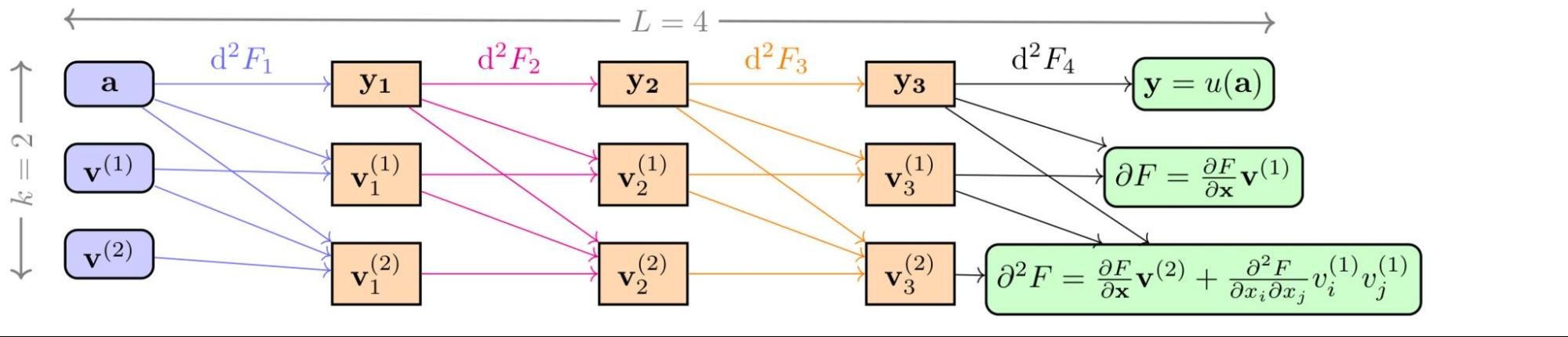
Em nosso artigo recente, "Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators", que recebeu o prêmio de melhor artigo na NeurIPS 2024, demonstramos como essa abordagem poderia ser usada. Mostramos que, usando o modo Taylor do JAX, podíamos criar um algoritmo para extrair essas derivadas parciais de ordem superior com eficiência. A ideia central era utilizar a DA do modo Taylor para computar com eficiência as contrações de tensores de derivadas de ordem superior que aparecem em EDPs. Ao construir vetores tangentes aleatórios especiais (ou "jets"), podíamos obter uma estimativa imparcial de um operador diferencial arbitrariamente complexo em uma única passagem direta e eficiente.
Os resultados foram dramáticos. Com nosso método STDE no JAX, alcançamos uma >aceleração de 1.000 vezes e uma >redução de memória de 30 vezes em comparação com os métodos de linha de base. Esse ganho de eficiência nos permitiu resolver uma EDP de 1 milhão de dimensões em apenas 8 minutos em uma única GPU NVIDIA A100, uma tarefa que antes era impraticável.
Isso simplesmente não teria sido possível com um framework voltado apenas para cargas de trabalho de aprendizado de máquina padrão. Outros frameworks são altamente otimizados para retropropagação, mas colocam menos foco na representação de grafos computacionais de ponta a ponta do que o JAX. Isso ajuda o JAX a brilhar com operações como transposição de uma função ou implementação da diferenciação do modo Taylor de ordem superior.
Além do modo Taylor, o design modular e o suporte do JAX a tipos de dados gerais e transformações de funções são fundamentais para nossa pesquisa. Em outro trabalho, "Automatic Functional Differentiation in JAX", até generalizamos o JAX para lidar com vetores de dimensão infinita (funções no espaço de Hilbert), descrevendo-os como uma matriz personalizada e registrando-os com o JAX. Isso nos permite reutilizar o maquinário existente para calcular derivadas variacionais para funcionais e operadores, uma funcionalidade que está completamente fora do alcance de outros frameworks.
Por essas razões, adotamos o JAX não apenas para esse projeto, mas para uma ampla gama de nossas pesquisas em áreas como a química quântica. Seu design fundamental como um sistema geral, extensível e simbolicamente poderoso faz dele a escolha ideal para ultrapassar as fronteiras da computação científica. Achamos que é importante que a comunidade científica conheça essa capacidade.
A experiência de Zekun e Min demonstra o poder e a flexibilidade do JAX. O método STDE desenvolvido por eles usando o JAX é uma contribuição significativa para o campo do aprendizado de máquina baseado na física, tornando possível lidar com uma classe de problemas que antes eram impraticáveis. Incentivamos você a ler o artigo premiado da dupla para se aprofundar nos detalhes técnicos e explorar a biblioteca STDE de código aberto deles no GitHub, uma adição fantástica ao cenário das ferramentas científicas nativas do JAX.
Histórias como essa destacam uma tendência crescente: o JAX é muito mais do que uma ferramenta para aprendizado profundo; é uma biblioteca fundamental para programação diferenciável que está capacitando uma nova geração de descobertas científicas. A equipe do JAX no Google está empenhada em apoiar e fazer crescer esse ecossistema vibrante, e isso começa ouvindo diretamente o que você pensa.
Mal podemos esperar para trabalhar com você e criar a próxima geração de ferramentas de computação científica. Entre em contato com a equipe para compartilhar seu trabalho ou para discutir o que você precisa no JAX.
Agradecemos sinceramente a Zekun e Min por compartilharem sua jornada inspiradora conosco.
Referência
Shi, Z., Hu, Z., Lin, M., & Kawaguchi, K. (2025). Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators. Advances in Neural Information Processing Systems, 37.
Lin, M. (2023). Automatic Functional Differentiation in JAX. The Twelfth International Conference on Learning Representations.
