JAX は、評価の高い大規模 AI モデル開発向けフレームワークとしてよく知られていますが、さまざまな科学分野でも急速に導入が進んでいます。特に、物理学に基づいた機械学習のような計算集約型の分野での利用拡大に大きな期待が寄せられています。JAX は高階関数群である合成可能な変換をサポートしています。たとえば、grad は関数を入力として受け取り、その勾配を計算する別の関数を返します。重要なのは、これらの変換を自由に入れ子にする(合成する)ことができる点です。この設計により、JAX は高次導関数やその他の複雑な変換に特に有効になっています。
先日、シンガポール国立大学や SEA AI Lab の研究者、Zekun Shi 氏や Min Lin 氏とお話しをする機会がありました。彼らの経験は、JAX が科学研究における基本的な課題、特に複雑な偏微分方程式(PDE)を解く際に直面する計算の崖にどのように対処できるかを明確に示しています。従来のフレームワークの限界に挑むことから始まり、JAX 独自のテイラー方式自動微分の活用に至るまでの彼らの道のりは、多くの研究者の共感を呼ぶでしょう。
私たちの研究は、ニューラル ネットワークを使用して高階 PDE を解くという科学コンピューティングの困難な分野に焦点を当てています。ニューラル ネットワークは普遍的な関数近似器であり、有限要素などの従来の方法に代わる手段として有望視されています。しかし、ニューラル ネットワークを使用して PDE を解く際の主なハードルは、混合偏微分など、ときには 4 次以上の高次導関数を評価する必要があることです。
主にバックプロパゲーションを介したトレーニング モデル向けに最適化されている標準的なディープ ラーニング フレームワークは、このタスクには適していません。高次導関数の計算には膨大なコストがかかるためです。高次導関数に対して繰り返しバックプロパゲーション(バックワード モード AD)を適用するコストは、導関数の階数(k)に対して指数関数的に、定義域の次元(d)に対して多項式的に増加します。この「次元の呪い」と導関数の階数の指数関数的な増加によって、大規模で複雑な現実世界の問題に取り組むことが事実上不可能になります。

ディープ ラーニングには他にも人気のあるライブラリがありますが、私たちの研究にはより基本的な機能、テイラー方式自動微分(AD)が必要でした。そこで JAX が私たちにとってのゲーム チェンジャーになりました。
JAX の主なアーキテクチャ上の特長は、Python コードをトレースすることによって実装され、パフォーマンス重視でコンパイルされた強力な関数表現と変換メカニズムです。このシステムは汎用性が高い設計になっており、ジャストインタイム コンパイルから標準的な導関数の計算まで、さまざまな用途に対応できます。この基礎となる柔軟性の高さが、他のフレームワークでは簡単には達成できない高度な操作を可能にしています。私たちにとって重要な用途は、テイラー方式 AD のサポートでした。これは、この独自アーキテクチャの直接的かつ強力な成果であり、JAX を科学研究に最適なツールにしています。テイラー方式 AD は、関数のテイラー級数展開を前方に押し出すことで高次導関数の効率的な計算を可能にします。これにより、コストが大きいバックプロパゲーションを繰り返さなくても、1 回の計算で高次導関数を効率的に計算できます。そのおかげで、Stochastic Taylor Derivative Estimator(STDE)というアルゴリズムを開発し、あらゆる微分作用素を効率的にランダム化し、推定できるようになりました。
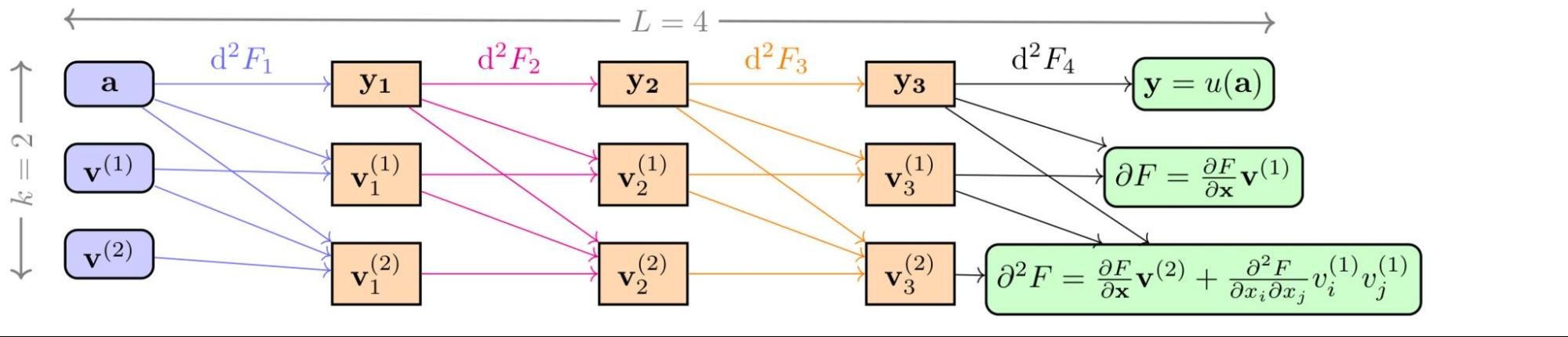
NeurIPS 2024 で最優秀論文賞を受賞した私たちの最近の論文「Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators」では、このアプローチをどのように使用できるかを実証しました。JAX のテイラー方式を使用することで、これらの高次偏微分を効率的に抽出するアルゴリズムを作成できることを示しました。中核となるアイデアは、テイラー方式 AD を活用して、PDE に現れる高次導関数テンソルの収縮を効率的に計算することでした。特殊なランダム接線ベクトル(または「ジェット」)を構築することで、効率的な前方計算 1 回で、任意に複雑な微分作用素を偏りなく推定できるようになりました。
結果は劇的でした。JAX の STDE メソッドを使用することで、ベースライン メソッドと比較して >1000 倍のスピードアップと >30 倍のメモリ削減を達成しました。この効率向上により、1 基の NVIDIA A 100 GPU を使い、わずか 8 分で 100 万次元の PDE を解けました。これは、以前は手に負えなかったタスクです。
これは、標準的な機械学習ワークロードのみを対象としたフレームワークでは不可能でした。他のフレームワークは、バックプロパゲーション向けに高度に最適化されていますが、JAX ほどエンドツーエンドの計算グラフ表現は重視されていません。だからこそ JAX は、関数の転置や高階テイラー方式微分の実装などの操作で強みを発揮します。
テイラー方式だけでなく、JAX のモジュール設計や、一般的なデータ型と関数変換のサポートも、私たちの研究にとって重要です。別の研究「Automatic Functional Differentiation in JAX」では、JAX を一般化して、無限次元ベクトル(ヒルベルト空間の関数)を、カスタム配列として記述して JAX に登録することで処理できるようにしました。これにより、既存の仕組みを再利用して、関数や作用素の変分導関数を計算できます。これは、他のフレームワークでは完全に手の届かない機能です。
これらの理由から、JAX はこのプロジェクトだけでなく、量子化学などの幅広い分野の研究にも採用されています。汎用性と拡張性に優れ、記号的に処理できる強力なシステムとしてのその基本設計は、科学計算のフロンティアを切り開く理想的な選択肢となっています。私たちは、この機能について科学コミュニティに周知することが重要であると考えています。
Zekun 氏と Min 氏の経験は、JAX の力と柔軟性を実証しています。JAX を使用して開発された STDE メソッドは、物理学に基づいた機械学習の分野に大きく貢献しており、以前は手に負えなかった一連の問題への対処を可能にします。受賞歴のある論文を読んで、技術的な詳細を深く掘り下げ、GitHub 上のオープンソースの STDE ライブラリを参照することをおすすめします。これは、JAX ネイティブの科学ツールの界隈に素晴らしい仲間が加わったことを意味します。
このような事例から、ある傾向が浮き彫りになります。JAX はディープ ラーニング用のツールに留まらず、新世代の科学的発見を支える微分可能プログラミングの基礎ライブラリにもなるということです。Google の JAX チームは、この活気に満ちたエコシステムをサポートし成長させることに全力を注いでいますが、それは皆様から直接話を聞くことから始まります。
皆様と協力して、次世代の科学計算ツールを構築できることを楽しみにしています。JAX のチームまでご連絡のうえ、皆様の仕事の内容や、JAX に何が必要かをお聞かせください。
有益な取り組みについて共有してくれた Zekun 氏と Min 氏に心から感謝します。
リファレンス
Shi, Z.、Hu, Z.、Lin, M.、&Kawaguchi, K.、2025 年、Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators。 Advances in Neural Information Processing Systems 37.
Lin, M.(2023 年)、Automatic Functional Differentiation in JAX。 The Twelfth International Conference on Learning Representations.