
While JAX is well known as a popular framework for large scale AI model development, it is also gaining rapid adoption in a wider set of scientific domains. We are particularly excited to see its growing use in computationally intensive fields like physics-informed machine learning. JAX supports composable transformations, a set of higher-order functions. For example, grad takes a function as input and returns another function which computes its gradient—and crucially, you can nest (compose) these transformations freely. This design is what makes JAX especially elegant for higher-order derivatives and other complex transformations.
Recently, I had the pleasure of speaking with Zekun Shi and Min Lin, researchers from the National University of Singapore and Sea AI Lab. Their experience clearly illustrates how JAX can address fundamental challenges in scientific research, particularly around the computational cliff faced when solving complex Partial Differential Equations (PDEs). Their journey from grappling with the limitations of traditional frameworks to harnessing JAX's unique Taylor mode automatic differentiation is a story that will resonate with many researchers.
Our work focuses on a challenging area of scientific computing: using neural networks to solve high-order PDEs. Neural networks are universal function approximators, which makes them a promising alternative to traditional methods like finite elements. However, a major hurdle in solving PDEs with a neural network is that you need to evaluate its high-order derivatives, sometimes up to the fourth order or even higher, including mixed partial derivatives.
Standard deep learning frameworks, which are primarily optimized for training models via backpropagation, are not well-suited for this task as computing high-order derivatives is incredibly expensive. The cost of applying back-propagation (backward mode AD) repeatedly for high-order derivatives scales exponentially with the derivative order (k) and polynomially with the domain dimension (d). This "curse of dimensionality" and exponential scaling in derivative order make it practically impossible to tackle large, complex, real-world problems.

While there are other popular libraries for Deep Learning, our research required a more fundamental capability: Taylor mode automatic differentiation (AD). JAX was a game-changer for us.
The key architectural distinction of JAX is its powerful function representation and transformation mechanism, implemented by tracing Python code and compiled for high performance. This system is designed with such generality that it enables a versatile range of applications, from just-in-time compilation to computing standard derivatives. It is this underlying flexibility that allows for advanced operations not easily achievable in other frameworks. For us, the crucial application was the support for Taylor mode AD, which we learned is a direct and powerful result of this unique architecture, making JAX perfectly equipped for our scientific work. Taylor mode AD enables the efficient computation of high-order derivatives by pushing forward a function's Taylor series expansion and efficiently computing high-order derivatives in a single pass rather than through repeated, costly back-propagation. This enabled us to develop an algorithm, the Stochastic Taylor Derivative Estimator (STDE), to efficiently randomize and estimate any differential operator.
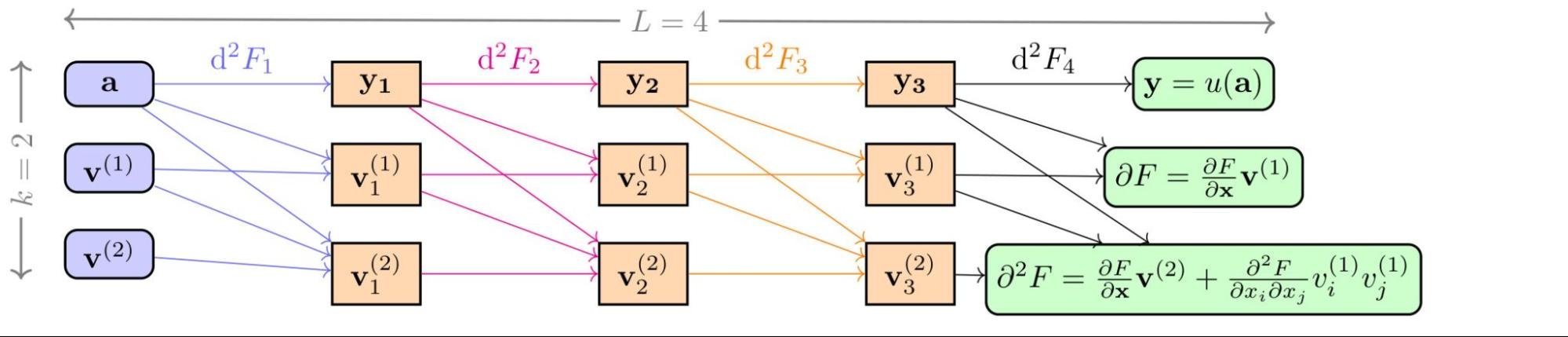
In our recent paper, "Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators", which received a Best Paper Award at NeurIPS 2024, we demonstrated how this approach could be used. We showed that by using JAX's Taylor mode, we could craft an algorithm to extract these high-order partial derivatives efficiently. The core idea was to leverage Taylor mode AD to efficiently compute contractions of high-order derivative tensors that appear in PDEs. By constructing special random tangent vectors (or "jets"), we could get an unbiased estimate of an arbitrarily complex differential operator in a single, efficient forward pass.
The results were dramatic. Using our STDE method in JAX, we achieved a >1000x speed-up and >30x memory reduction compared to baseline methods. This efficiency gain allowed us to solve a 1-million-dimensional PDE in just 8 minutes on a single NVIDIA A100 GPU, a task that was previously intractable.
This simply wouldn't have been possible with a framework geared only towards standard machine learning workloads. Other frameworks are highly optimized for backpropagation, but place less focus on end-to-end computational graph representation than JAX. That helps JAX shine with operations like transposing a function or implementing higher-order Taylor mode differentiation.
Beyond Taylor mode, JAX's modular design and support for general data types and function transformations are critical for our research. In another work, “Automatic Functional Differentiation in JAX”, we've even generalized JAX to handle infinite-dimensional vectors (functions in Hilbert space) by describing them as a custom array and registering them with JAX. This allows us to reuse the existing machinery to calculate variational derivatives for functionals and operators, a functionality that is completely out of reach for other frameworks.
For these reasons, we have adopted JAX not just for this project, but for a wide range of our research in areas like quantum chemistry. Its fundamental design as a general, extensible, and symbolically powerful system makes it the ideal choice for pushing the frontiers of scientific computation. We believe it's important for the scientific community to know about these capabilities.
Zekun and Min's experience demonstrates the power and flexibility of JAX. Their STDE method developed using JAX is a significant contribution to the field of physics-informed machine learning, making it possible to tackle a class of problems that were previously intractable. We encourage you to read their award-winning paper to dive deeper into the technical details and explore their open-source STDE library on GitHub, which is a fantastic addition to the landscape of JAX-native scientific tools.
Stories like this highlight a growing trend: JAX is much more than a tool for deep learning; it's a foundational library for differentiable programming that is empowering a new generation of scientific discovery. The JAX team at Google is committed to supporting and growing this vibrant ecosystem, and that starts with hearing directly from you.
We are excited to partner with you to build the next generation of scientific computational tools. Please reach out to the team to share your work or discuss what you need from JAX.
Sincere thanks to Zekun and Min for sharing their insightful journey with us.
Shi, Z., Hu, Z., Lin, M., & Kawaguchi, K. (2025). Stochastic Taylor Derivative Estimator: Efficient amortization for arbitrary differential operators. Advances in Neural Information Processing Systems, 37.
Lin, M. (2023). Automatic Functional Differentiation in JAX. The Twelfth International Conference on Learning Representations.